Editor’s note: The following is from a transcript of a forgotten speech given in Tokyo in 1978 by W. Edwards Deming for the Union of Japanese Scientists and Engineers (JUSE). Because the original was a poor photocopy, there are small portions of text that could not be transcribed. Transcript courtesy of Mike McLean.
The spectacular leap in quality of most Japanese manufactured products, from third-rate to top quality and dependability, with astounding economy in production, started off in 1950 with a meteoric flash, and still continues. The whole world knows about Japanese quality and the sudden surge upward that began in 1950, but few people have any idea how it happened.
It seems worthwhile to collect in one place the statistical principles of administration that made possible the revolution of quality in Japan, as even at this date, most of these principles are not generally understood or practiced in America. It is for this reason that the title speaks of new principles.
The relative importance of some of the principles explained here have of course changed over the years since 1950. Some principles stated here have emerged as corollaries of earlier principles. Other corollaries could be added, almost without end.
The leap forward in quality in Japan was no accident. It was success that followed concerted, determined, methodical effort, throughout all Japanese industry, at all levels of production, including, of course, management, to put the statistical methods to work. Return visits, along with courses at different levels for management, engineers, and foremen, arranged by the Union of Japanese Scientists and Engineers, guided and welded these efforts. It may be that such a concerted movement is possible only in Japan.
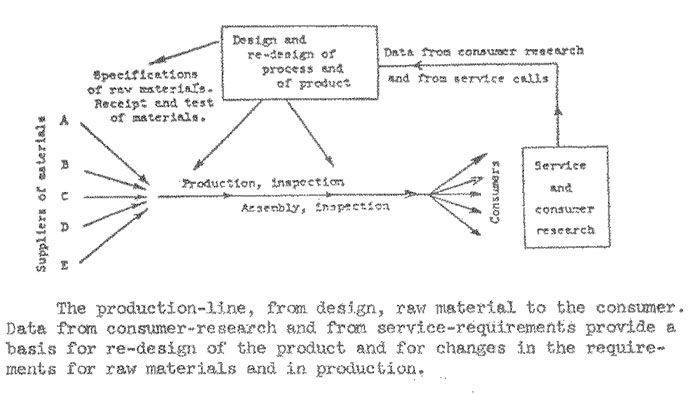
It will be obvious that recognition of problems in quality, uniformity, and economy, and evaluation of attempts to solve them, require statistical methods and statistical thinking. Statistical methods cover every step in the production line, from specifications and tests of incoming materials, to tests of product in service, to consumer research, design, and redesign of product. This is why, as [Walter A.] Shewhart said, the statistical control of quality is the broadest term possible for the problems of economic production.
Principle 1
It is demoralizing and costly to call to the attention of a production worker a defective item that he has made, when he is in a state of statistical control with respect to the cause of that defect.1 To do so would help him not at all, as he is, in effect, drawing blindfolded, samples of beads, white and black, from a bowl of black and white beads thoroughly mixed. He cannot govern the random appearance of black beads in his samples, his product; he cannot beat the system. He is handicapped by the proportion of black beads in the system. Only the management can change the portion of black beads in the bowl.
In fact, if you call his attention to a defective item when his work is in statistical control with respect to the cause of that defect, he will try to modify his procedure… [text lost] hoping vainly for improvement. The result of his modification will be… [text lost] an increase in the variability of his output—backfire that defeats his efforts.
The argument that a production worker has a right to know how he is doing and that he cannot know unless he sees the defective items that he produces, is one of the common fallacies of administration as taught today in schools of business. The fallacy explained here arises from failure to understand the best principles of administration.
Principle 2
It is better to shift to a totally different job, a worker that has developed statistical control of his work in his present job, but whose output in quality or in quantity is unsatisfactory.
| |
Principle 3
It is possible to train and retrain a worker, who has not yet achieved statistical control of his work.
Principle 4
Maximum and minimum limits for the specification of a product are by themselves a costly and unsatisfactory guide to the production worker. Thus, specification limits for an outside diameter to lie between 1.001 and 1.002 cm tell the production worker that a diameter of 1.0012 cm meets the specification, but it is no help to him in an attempt to produce fewer defectives and to increase his production, both of which he can accomplish with less effort with the aid of statistical methods. (Stated years ago by Dr. Shewhart.)
Principle 5
His job description should therefore, for best economy, require him to achieve statistical control of his work with the distribution of individual items that meet the specifications. Under this system, his output will meet the specifications without the high cost of detailed inspection. Workers that are in statistical control but whose output is unsatisfactory can be transferred and trained in other work.
Principle 6
Good quality does not necessarily mean high quality. It means mainly uniformity and dependability, at low cost, with quality suited to the market.
Principle 7
Variation in a quality characteristic causes a loss, even though the variation be not enough to exceed the specifications. With greater uniformity, the manufacturer may be able to economize on the production process, such as to curtail some operations, or to use cheaper raw materials, and still meet specifications. Thus, greater uniformity enables a) a manufacturer and his customer—both of them—to achieve greater economy; and b) provides a better basis for doing business together.
Examples abound, but it may not be so well known that uniformity in agricultural products is also important to economic processing of foods and other derivatives.2
Principle 8
In a state of chaos (poor supervision, bad management, nothing in statistical control), it is impossible for a production worker to develop his potential ability and capacity for uniformity or for quantity.
Statistical methods, such as a control chart, provide signals that indicate the existence of a special cause that requires corrective action.
Principle 9
Causes of high cost of production, with loss of competitive position, may be usefully subsumed under two categories:
Faults of the system | Special causes |
85% | 15% |
These faults stay in the system until reduced by management. Their combined effect is usually easy to measure. Some individual causes will be isolated by judgment. Others may be identified by experiment; some by study of records on operations and materials. | These causes are specific to a certain worker or to a machine. A statistical signal detects the existence of a special cause, which the worker can usually identify and correct. |
The percentages shown only indicate that, in my experience, problems of the system overshadow special causes. Design of product, and testing in service, are part of the system and are the responsibilities of management.
Common causes get their name from the fact that they are common to a whole group of workers: They belong to the system.
No improvement of the system, nor any reduction of special causes of variation and trouble, will take place unless management attacks common causes.
Confusion between the two types of cause leads to frustration at all levels, and leads to greater variability and to higher costs—exactly contrary to what is needed.
Principle 10
Fortunately, this confusion can be eliminated with almost unerring accuracy. Simple statistical techniques such as distributions, run charts, Shewhart control charts, all explained in books, provide signals that tell the operator when to take action to improve the uniformity of his work. They also tell him when to leave his process alone.
Principle 11
These simple statistical techniques minimize the net cost of two common mistakes:
1. Over adjusting, looking too often for a special cause, and taking action that only increases the variation and defeats the aim
2. Doing too little or nothing about special causes
It is easy to avoid completely either mistake. One can avoid No. 1 by doing nothing about special causes, thus committing No. 2 as often as possible. The result is chaos. Or, he can avoid No. 2 by taking action on the slightest indication of variation up or down. The result is an increase in variation and more chaos.
Statistical methods provide the only economic way to achieve stability and to minimize the net loss from both mistakes.
What is not in the books, nor known or generally amongst quality-control engineers, is that the same charts that send statistical signals to the production worker also provide for management a measure of the totality of fault that belongs to the system itself.3
Principle 12
The first step of any process of manufacture, or of measurement, is to achieve statistical control of one of the main characteristics of the product, then another, and another. Once statistical control of the main quality characteristics of a process is achieved, the process is ready for the next step—improvement, the responsibility of management.
The first step of any process of manufacture, or of measurement, is to achieve statistical control of one of the main characteristics of the product; then another, and another.
An attempt to evaluate the effect of steps taken to reduce common causes will be risky and misleading unless some of the processes have been brought into a state of statistical control.
The problems of the system remain even though statistical control of the most important quality characteristics of the product has been achieved (as long taught by Dr. [Joseph M.] Juran). Again, the problems of the system are problems for management.
Principle 13
A mechanical governor that merely holds quality characteristic within specifications does not achieve better uniformity for tomorrow and the economic benefits thereof. It does not improve the system. Mechanical governors may be used advantageously, in conjunction with computing equipment, to plot charts to calculate statistical characteristics that will provide a signal to the supervisor to indicate when a special cause of variation calls for corrective adjustment.
Principle 14
Management is not doing the job of management, unless there be a system of meaningful records, with statistical evaluation, to learn what proportion of recognized problems belong to the system, and hence to management.
The usual claim of management, in the absence of statistical methods, that “we are doing everything that we know of to improve quality and to decrease costs,” though ever so true, is only a confession of wishful thinking without benefit of knowledge of statistical principles of administration.
A typical statement from management might run like this: “I understand enough about quality control to manage it effectively from my office as president.” Shallowness of understanding only manifests itself when trouble occurs.4
The usual supposition on the part of American management is that the production workers are responsible for all the problems of production and of quality. Management, in the absence of statistical methods, proceeds on the theorem that if the workers made no errors, there would be no trouble. This elegant theorem does not improve uniformity of product or reduce losses. It is a costly attitude. It conceals the responsibilities and the opportunities of management and guarantees continuation of trouble.
The fault behind the recall of automobiles for correction, familiar to everyone, whenever something was admittedly wrong is not chargeable to workmanship, but to design, the system, hence the fault of management.
The boost in morale of the production worker, if he were to perceive a genuine attempt on the part of management to improve the system and to hold the production worker responsible only for what the production worker is responsible for and can govern, and not for handicaps placed on him by the system, would be hard to overestimate.
Principle 15
A process has an identity and a predictable capability only if it is in a state of statistical control. In this state, the main quality characteristics of the product will dependably fall tomorrow within predictable limits. Output can be predicted, likewise cost of production.
From “Quick Review of Some New Principles of Administration”
Principle 16
The consumer is the most important point on the production line. Consumer research and testing in service are statistical problems.
Principle 17
Performance of a product is the result of interaction between three participants: 1) the product itself; 2) the user and how he uses the product, how the customer installs it, how he takes care of it, and the conditions of use (example: customer permitted dirt to fall into roller bearing); and 3) instructions for use, training of customer, service provided for repairs, training of repairmen, and availability of spare parts.
The manufacturer of a piece of equipment on which service records are kept may learn continually by studies of the records how the total package of trouble is apportioned amongst the three components and how to improve most economically the performance of his product.
Suggestions:
1. Make frequency distributions of diagnosis of trouble by type of customer, by serviceman, by type of equipment. Some random switching of servicemen amongst customers and types of equipment would provide a basis for improvement in the training of servicemen.
2. Same by customer, by type of equipment. The results would show what type of customer and what conditions of use are likely to give satisfaction, and which are likely to give dissatisfaction.
3. Trends in the amount of trouble, by kind of trouble, by kind of equipment.
Principle 18
Criteria for test of a unit of product, by which to declare it conforming or not conforming to specifications, are totally different in concept and operational meaning from criteria from judgement of the performance of the product in service.5
Principle 19
On-time performance of delivery of product exhibits early delivery some days and late delivery some days.
This principle came to my mind one day in Japan as I stepped onto the platform and observed the time to be 10 seconds before the scheduled time of arrival. “Of course,” I observed, “it has to be ahead half the time, and behind half the time, if its performance is on time.”
Principle 20
Management faces two types of problems in the making and marketing a product:6
A. What to do with product already made. Is it fit to send out to the market or to a designated customer?
B. How to improve future product.
Problem A is ever with the manufacturer: What to do with today’s product? Work on problem B is investment. Each degree of success in problem B simplifies problem A in future days.
There was a time when quality control consisted of problem A to the near exclusion of problem B. It was supposed that inspection of final product to screen out defective items would guarantee that only good items went out to the market or to a designated customer.
It is now known that no amount of inspection of product at the end of the line can guarantee quality of performance of product. Some defective items will slip through and cause ill will. There is, moreover, at the end of the line, continual pressure to waive requirements in order to avoid loss of time and the expense of rework or replacement. The greater be the reliance on inspection, the greater will be the proportion of defective items that slip through to the market.
It is now known that no amount of inspection of product at the end of the line can guarantee quality of performance of product.
The idea that the solution lay in inspection and more inspection gave way here and there to the idea that something should be done with the process to reduce the proportion of defectives made.
Statistical acceptance procedures should be the first thought in problem A. It is fairly simple, once a decision is made on the maximum allowable proportion of defectives that shall be permitted to go out, to find in the Dodge-Romig tables the plan of sampling and acceptance that is most economical. Inspection of finished product carried out under an appropriate statistical plan a) guarantees an average outgoing quality limit; and b) furnishes a record that shows how the process is doing, and whether its quality is level, declining, or improving.
Statistical methods offer also the economical approach to problem B, improvement of the process.
Principle 21
The cost of producing a few units of product and testing them do not give enough information on which to predict the cost of production even when combined with a forecast of the market. One must know also how the customer will test lots for acceptance. Must every piece conform to specifications? (Impossible, of course, if the test is destructive.) Or will the customer use a plan of acceptance that does not require 100-percent conformance?
Principle 22
Measurement, simple or complex, is a production process.7 The product is numbers, called measurements. There is no identifiable system of measurement, unless it is in statistical control, including interchange of observers. Statistical control is not a matter of opinion but of satisfaction of certain statistical tests for randomness.
It has been my observation that unreliable instruments and unreliable measurements are the source of a great deal of trouble and friction in production. Is the product defective, or are the measurements wrong?
Any manufacturer has troubles daily with differences between his own results of measurement and those that his customer makes; between his standard measures and reagents and his customer’s standard measures and reagents.
Any processor of food can recall horrifying experiences in which product already distributed, or ready for distribution, has been condemned, temporarily at least, because of false positive results of tests, later traced to contamination in his own laboratory.
Principle 23
Due care in manufacture cannot be defined operationally; hence, any requirements of due care in manufacture can have no legal force. Care in manufacture, however, can be defined and measured. Evidence of care is provided by records of tests, in the form of meaningful data (which might take the form of charts and statistical calculations), supplemented by records of corrective action and the result. Instructions for use of the product, and warnings of misuse, are part of the record that establishes the amount of care taken on the part of the manufacturer.
Principle 24
The practice of instituting a so-called award of merit to a production worker or to a group of workers for best performance (highest sales, fewest defectives, greatest production) over a recent period may well be demoralizing unless the award is based on satisfactory statistical measurement that will distinguish good performance from plain luck. If the award is not based on a statistical measure of performance, then the system of award is only a lottery. There is no harm in a lottery, so far as I know, if it is called a lottery, but a lottery can do a lot of harm if it is called merit. The results will be decreased production, poorer quality, and dissatisfaction with the job. It is costly to confuse good luck with merit earned.
Principle 25
Statistical methods are not installed in a company or in a governmental organization. Statistical methods grow from the roots of knowledge and experience. Knowledge of statistical theory is the foundation. There are no cookbook-guaranteed recipes to follow.
References
1. Principles 1–17 were described in more detail in my paper, “On some statistical aids to economic production,” Interfaces, Vol. 5, No. 4, Aug. 1975: pp. 1–15; also in “My view of quality control in Japan,” Reports of Statistical Applications Research, vol. 22, No. 2, June 1975: pp. 73–80.
2. Smith, Richard D. “Saving the super crops,” The Sciences, Vol. 16, 1976: pp. 13–18.
3. For examples, see W. Edwards Deming, “On some statistical aids toward economic production,” Interfaces, vol. 5, Aug. 1975: pp. 1–15.
4. Golomski, William. “Departmental size,” Quality Progress, Aug. 1976, p. 13.
5. This principle was continually emphasized by Harold F. Dodge, certainly as early as 1944.
6. This principle was stated by George Edwards of the Bell Telephone Laboratories certainly as early as 1942. It pervaded the work of Harold F. Dodge in his contributions to acceptance sampling and throughout his long service as chairman of Committee E-11 of the American Society for Testing and Materials.
7. • Shewhart, Walter A. “Statistical method from the viewpoint of quality control,” The Graduate School, Department of Agriculture, Washington, 1939; pp. 110–119.
• Ku, Harry H. “Precision measurement and calibration,” National Bureau of Standards, Washington, vol. 1, Publication 300, 1969.
• Cameron, Joseph M. “Measurement Assurance,” National Bureau of Standards, Washington, Bulletin No. NBSIR 77.1240, 1977.
ABOUT THE AUTHOR
W. Edwards Deming
W. Edwards Deming was an American engineer, statistician, professor, author, lecturer, and management consultant. While working under Gen. Douglas MacArthur as a census consultant to the Japanese government, he was contacted by the Union of Japanese Scientists and Engineers (JUSE) to talk directly to Japanese business leaders, not about SPC, but about his theories of management, and he returned to Japan for many years to consult. Later, he became a professor at New York University, while engaged as an independent consultant in Washington, DC. Deming was the author of Quality Productivity and Competitive Position, Out of the Crisis (1982–1986), and The New Economics for Industry, Government, Education (1993), as well as books on statistics and sampling.
' xlink:href='%23b'/%3e%3cuse fill='black' filter='url(%23c)' xlink:href='%23b'/%3e%3cpath fill='white' d='M12.162 7.338c.176.123.338.245.338.674 0 .43-.229.604-.474.725a.73.73 0 01.089.546c-.077.344-.392.611-.672.69.121.194.159.385.015.62-.185.295-.346.407-1.058.407H7.5c-.988 0-1.5-.546-1.5-1V7.665c0-1.23 1.467-2.275 1.467-3.13L7.361 3.47c-.005-.065.008-.224.058-.27.08-.079.301-.2.635-.2.218 0 .363.041.534.123.581.277.732.978.732 1.542 0 .271-.414 1.083-.47 1.364 0 0 .867-.192 1.879-.199 1.061-.006 1.749.19 1.749.842 0 .261-.219.523-.316.666zM3.6 7h.8a.6.6 0 01.6.6v3.8a.6.6 0 01-.6.6h-.8a.6.6 0 01-.6-.6V7.6a.6.6 0 01.6-.6z'/%3e%3c/g%3e%3c/svg%3e){kind=small}